Kernel methods (see for example (Shawe-Taylor and Cristianini, 2004)) are a powerful class of algorithms for pattern analysis that, exploiting the so called kernel functions, can operate in an implicit high-dimensional feature space without explicitly computing the coordinates of the data in that space. Most of the existing machine learning platforms provide kernel methods that operate only on vectorial data. On the contrary, KeLP has the fundamental advantage that there is no restriction on a specific data structure, and kernels directly operating on vectors, sequences, trees, graphs, or other structured data can be defined.
Furthermore, another appealing characteristic of KeLP is that complex kernels can be created by composing and combining simpler kernels. This allows to create richer similarity metrics in which different information from different Representations can be simultaneously exploited.
As shown in the figure below, KeLP completely supports the composition and combination mechanisms providing three abstractions of the Kernel class:
- DirectKernel: in computing the kernel similarity it operates directly on a specific Representation that it automatically extracts from the Examples to be compared. For instance, KeLP implements LinearKernel on Vector representations, and SubTreeKernel (Vishwanathan and Smola, 2002) (the SubSet Tree Kernel is a.k.a. Syntactic Kernel), and PartialTreeKernel (Moschitti, 2006) on TreeRepresentations.
- KernelComposition: it enriches the kernel similarity provided by any another kernel. Some KeLP implementations are PolynomialKernel, RbfKernel and NormalizationKernel.
- KernelCombination: it combines different kernels in a specific function. Some KeLP implementations are LinearKernelCombination and KernelMultiplication.
Finally, the class KernelOnPairs models kernels operating on ExamplePairs, which are pairs of objects, e.g., pairs of texts as in (Filice et al., 2015). It can be also used to design a ranking algorithm based on the preference kernel (Shen and Joshi, 2003), using the implementation PreferenceKernel.
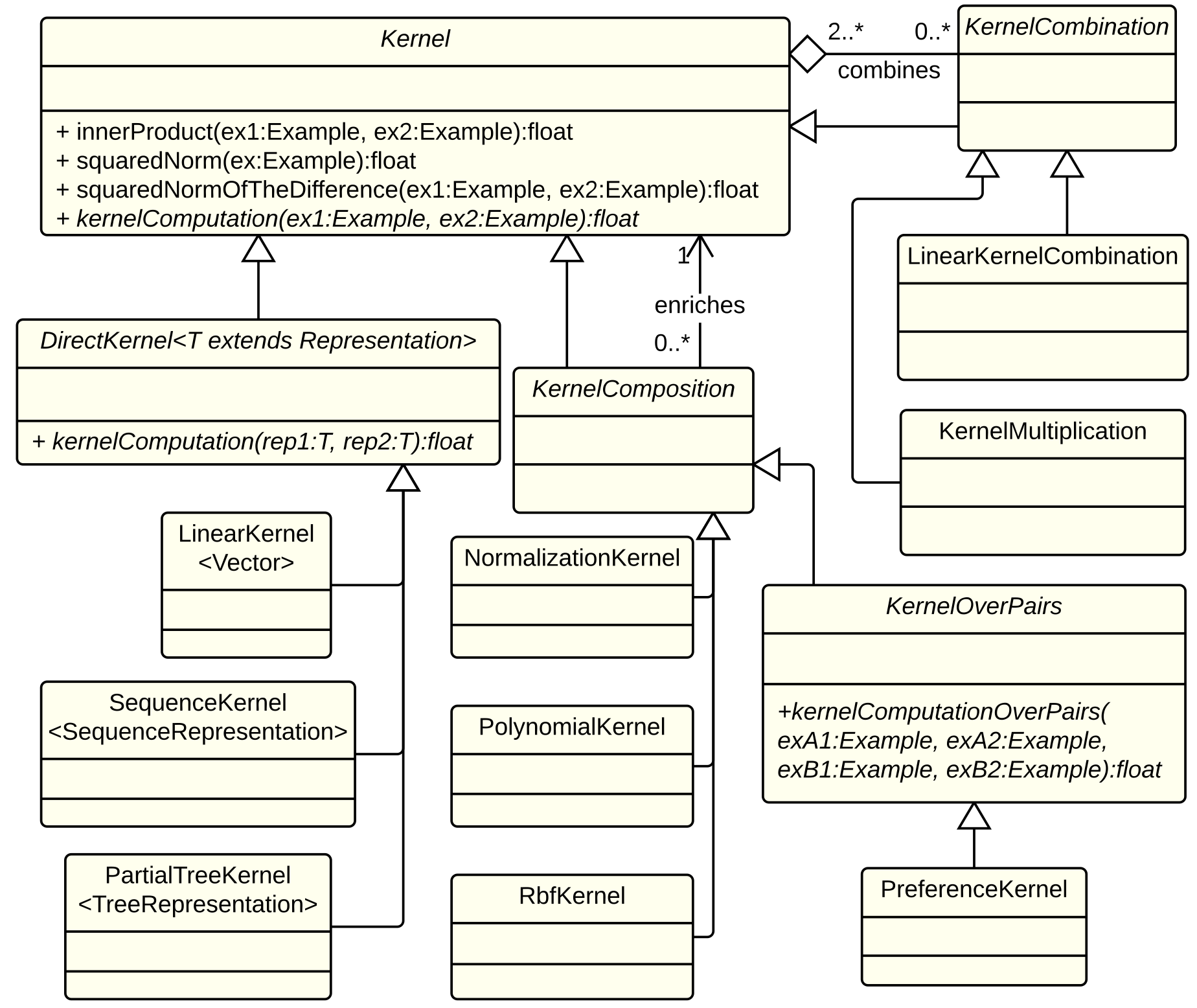
A simplified class diagram of the kernel taxonomy in KeLP.
Existing Kernels
- Kernels on Vectors:
- Linear Kernel
- Kernels on Sequences:
- Sequence Kernel
- Kernels on Trees:
- Subtree Kernel
- SubSet Tree Kernel
- Partial Tree Kernel
- Smoothed Partial Tree Kernel
- Compositionally Smoothed Partial Tree Kernel
- Kernels on Graphs:
- Shortest Path Kernel
- Weisfeiler-Lehman Subtree Kernel
- Kernel Compositions:
- Polynomial Kernel
- Radial Basis Function Kernel
- Normalization Kernel
- Kernel Combinations:
- Linear Kernel Combination
- Kernel Multiplication
- Kernels on Pairs:
- Preference Kernel
- Uncrossed Pairwise Sum Kernel
- Uncrossed Pairwise Product Kernel
- Pairwise Sum Kernel
- Pairwise Product Kernel
- Best Pairwise Alignment Kernel
References
Simone Filice, Giovanni Da San Martino and Alessandro Moschitti. Relational Information for Learning from Structured Text Pairs. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics, ACL 2015.
Alessandro Moschitti. Efficient convolution kernels for dependency and constituent syntactic trees. In ECML, Berlin, Germany, September 2006.
Libin Shen and Aravind K. Joshi. An svm based voting algorithm with application to parse reranking. In In Proc. of CoNLL 2003, pages 9–16, 2003
John Shawe-Taylor and Nello Cristianini. Kernel Methods for Pattern Analysis. Cambridge University Press, New York, NY, USA, 2004. ISBN 0521813972.
S.V.N. Vishwanathan and A.J. Smola. Fast kernels on strings and trees. In Proceedings of Neural Information Processing Systems, 2002.