February 13, 2017 kelp2

Sequence Learning

KeLP Sequence Learning

In this page we will learn how to use KeLP to build a sequential classifier. In fact, problems, where the involved input and outputs are sequences, are frequent in many fields. For example, problems like speech and hand-written recognition, protein secondary structure prediction or part-of-speech tagging, can be all treated with a sequence learning framework. In machine learning, such problems led to the definition of specific learning frameworks, where sequences are the main input/output of the algorithms. It makes the sequence learning different from classical pattern classification approaches. In the case of sequence problems, input/output sequences are strongly related each other.

Here we are going to provide a guide to adopt the sequence learning capabilities offered by the KeLP framework. In the next section, we are going to provide a brief introduction to the math behind the KeLP implementation, also described in (Castellucci et al., 2015).
If you are not interested in the math stuff, you can safely skip to the third section.

 

A hybrid discriminative-generative framework

The sequence labeling approach adopted in KeLP is based on an hybrid generative-discriminative framework. In particular, the model is made of a discriminative multi-classifier based on SVM, which is used to estimate the parameters of a Hidden Markov Model. The sequence classifier is obtained by applying the Viterbi algorithm on the trellis built starting from the SVM estimates. This formulation is inspired by the SVM-HMM classifier (Altun et al, 2003). The main difference is in the underlying optimization formulation, that in the case of SVM-HMM follows the Structured Learning paradigm proposed in (Joachims et al, 2009).
Let us consider an input sequence {\mathbf{x}=(x_{1} \dots x_{m})} \subseteq \mathcal{X} of observations, where x_i \in \mathbb{R}^n is a feature vector of some properties characterizing the instance x_i. Then, each sequence is associated to a label or tag sequence \mathbf{y}=(y_{1} \dots y_{m}) \in \mathcal{Y}^{+} (with y\in\Sigma and \|\Sigma\|=l). The aim of this model is to provide a learning schema, that is able to induce a classification function f that given \mathbf{x} is able to find the correct \mathbf{y}, i.e. f(\mathbf{x})=\mathbf{y}.

The final aim is to make the classification of an instance x_i dependent from the label assigned to the previous elements in a history of length k, i.e x_{i-k}, \dots, x_{i-1}. Given this history, a sequence of k labels can be retrieved, in the form y_{i-k}, \dots, y_{i-1}. In order to make the classification of x_i dependent also from the history, we can augment the feature vector of x_i introducing a vector of transitions \psi_{tr}({y_{i-k}, \dots, y_{i-1})}\in\mathbb{R}^k: it is a boolean vector where the dimensions corresponding to the k labels preceding the target element x_i are set to 1. It means that in the vector representations of an instance x_i, we add specific features representing the transitions corresponding to the current label sequence.
A projection function \phi(x_i) is thus defined to consider both the observations, i.e. \psi_{obs} and the transitions \psi_{tr} in a history of size k by concatenating the two representation, i.e.:

    \[x_{i}^{k} =\phi(x_i; y_{i-k}, \dots, y_{i-1})=\psi_{obs}(x_i)\ ||\ \psi_{tr}({y_{i-k}, \dots, y_{i-1})}\]

with x_{i}^{k}\in\mathbb{R}^{n+l} and \psi_{obs}(x_i) leaves intact the original feature space.

At training time, a One-Vs-All schema over the feature space derived by \phi can be adopted. In this way, for each y_j a linear classifier f_j (x_{i}^{k})=w_j \phi(x_i; y_{i-k}, \dots, y_{i-1})+b_j is learned. The \phi function is computed for each element x_i by exploiting the gold label sequences.
At classification time, all possible sequences \mathbf{y}\in\mathcal{Y^{+}} should be considered in order to determine the best labeling \hat{\mathbf{y}}=F(\mathbf{x},k), where k is the size of the history used to enrich x_i, that is:

(1)   \begin{align*} \hat{\mathbf{y}}&=F(\mathbf{x},k) = argmax_{\mathbf{y}\in\mathcal{Y^{+}}} \{\sum_{i = 1\dots m} f_j (x_{i}^{k}) \}= \\ &= argmax_{\mathbf{y}\in\mathcal{Y^{+}}} \{\sum_{i = 1\dots m} w_j \phi(x_i; y_{i-k}, \dots, y_{i-1})+b_j \} \end{align*}

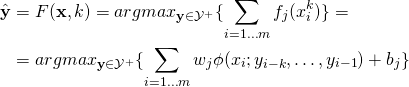
In order to reduce the computational cost, a \textit{Viterbi-like decoding algorithm} is adopted to derive the sequence, and thus build the augmented feature vectors through the \phi function.

 

An example of sequence learning in KeLP

The following example is based on the class available in the \texttt{kelp-full} project

and

In practice, given a dataset (a SequenceDataset) of SequenceExamples where each item in the sequence is represented as a set of Representations, the Sequence Learning framework in KeLP implements a learning process operating in the feature space. During the training step, each example is enriched to consider its history, in terms of classes assigned to the previous elements of the sequence. During the tagging process, the history of an example is dynamically estimated by a classifier and the entire sequence of labels is derived through a Viterbi decoding step combined with a beam search strategy.

The main data structure used in a Sequence Learning task is the SequenceDataset. It is made by a list of SequenceExample objects, each made by a list of Examples.
An Example models a single element of a sequence, for example a token in a part-of-speech tagging task. A SequenceExample models an entire sequence, e.g., the sentence in the part-of-speech tagging context. Finally, the SequenceDataset is used to model a dataset of sequences.

KeLP offers utility methods to load such object structure with a simple and intuitive interface, which is show in the following snippet:

It requires that the dataset is provided in a specific format, where each line is used to represent an element of a sequence along with its label, and each sequence is separated by a blank line. For example, the following snippet represents two sequences, the first composed by 5 elements and the second made by 4 elements. The first token of each SequenceExample is the label associated to that element of the sequence. In the following snippet the label of the first Example of the first sequence is 19, the label of the second Example of the sequence is 31, and so on…
Then, each Example is represented through a list of vectors, as the ones that has already been described at this page.

The KeLP sequential learning process requires the specification of a number of parameters.

Before the Viterbi decoding, a base learning algorithm is needed in order to classify each examples to one of the target classes. Each of the learning algorithms implementing the  ClassificationLearningAlgorithm interface (described at this page) can be adopted.

In the case that a learning algorithm operating in the primal space is adopted (such as the  DCDLearningAlgorithm) the SequenceClassificationLinearLearningAlgorithm needs to be instantiated, in combination with methods implementing a LinarMethod. This option is  preferred when no complex kernel is required. Moreover, it is useful for  efficiency reasons: the time/space required by the base learning algorithm in the training process depends on the number of Examples stored in the SequenceExamples; if this number grows, it is worth to adopt efficient method, such as DCDLearningAlgorithm or LiblinearLearningAlgorithm. In this case, the learning method can operate only over a geometrical representation (i.e, a Vector).

In order to use a kernel based method, the following code is required. Obviously, a kernel operating over the (possibile multiple) representations from the Examples in the SequenceExamples need to be implemented. It is suggested to adopt a KernelCache, that needs to be passed directly to the learning algorithm.

In both of the above cases, the \textttt{learn( )} method initiates the learning process, that will produce a dedicated prediction function, called SequencePredictionFunction.

The above prediction function can be easily used to tag a new sequence, obtaining a dedicated object, i.e., a SequencePrediction. The most sequence obtained by the Viterbi Decoding can be accessed via the \texttt{bestPath( )} method.

 

References

Castellucci Giuseppe, Andrea Vanzo, Danilo Croce, Roberto Basili. (2015) Context-aware Models for Twitter Sentiment Analysis. IJCoL vol. 1, n. 1 december 2015: Emerging Topics at the First Italian Conference on Computational Linguistics. 2015

Joachims, T., Finley, T., and Yu, C.-N. (2009). Cutting-plane training of structural svms. Machine Learning. 77(1), 27–59.

Altun, Y., Tsochantaridis, I., and Hofmann, T. (2003). Hidden Markov support vector machines. In Proceedings of the International Conference on Machine Learning.