February 13, 2017 kelp2

Using Advanced Kernels

This section shows some examples describing how to instantiate advanced kernel functions (such as Sequence Kernels, Tree Kernels and Graph Kernels) in learning algorithms.

Tree Kernels

Several NLP tasks require the explorations of complex semantic and syntactic phenomena. For instance, in Paraphrase Detection, verifying whether two sentences are valid paraphrases involves the analysis of some rewriting rules in which the syntax plays a fundamental role. In Question Answering, the syntactic information is crucial, as largely demonstrated in (Croce et al., 2011). In these scenarios, a possible solution is represented by the manual definition of an artificial feature set that is able to capture the syntactic and semantic aspects useful to solve a target problem. Determining how to exploit these features to generate robust predictive models is left to the learning algorithm. However, the definition of meaningful features is still a rather expensive and complicated process that requires a domain expert; moreover, every task has specific patterns that must be considered, making the underlying manual feature engineering an extremely complex and not portable process. Instead of trying to design a synthetic feature space, a more natural approach consists in applying kernel methods on structured representations of data objects, e.g., documents. A sentence s can be represented as a parse tree that takes into account the syntax of s.

Tree kernels (Collins and Duffy, 2001) can be employed to directly operate on such parse trees, evaluating the tree fragments shared by the input trees. Kernel-based learning algorithms, such as Support Vector Machines (Cortes and Vapnik 1995), can operate in order to automatically generate robust prediction models. Different tree representations embody different linguistic theories and may produce more or less effective syntactic/semantic feature spaces for a given task. Among the different variants discussed in (Croce et al. 2011), we first investigate in this example the Grammatical Relation Centered Tree (GRCT) illustrated below

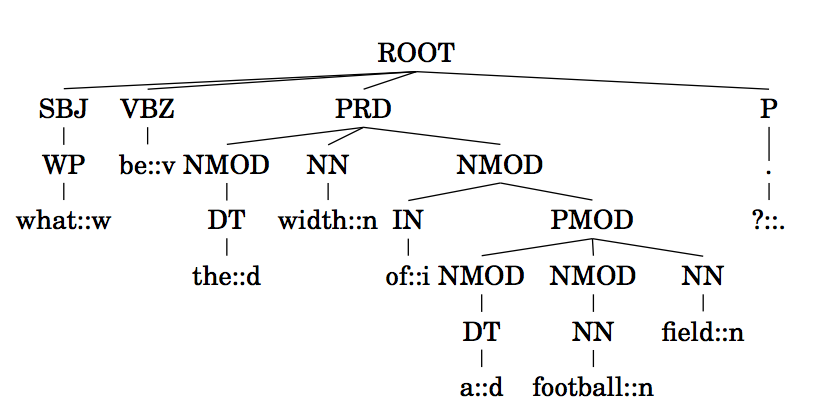
In a nutshell, given a sentence such as “What is the width of a football field ? ” we can use a natural language parser, such as Stanford Parser to extract a Dependency Parse tree, such as

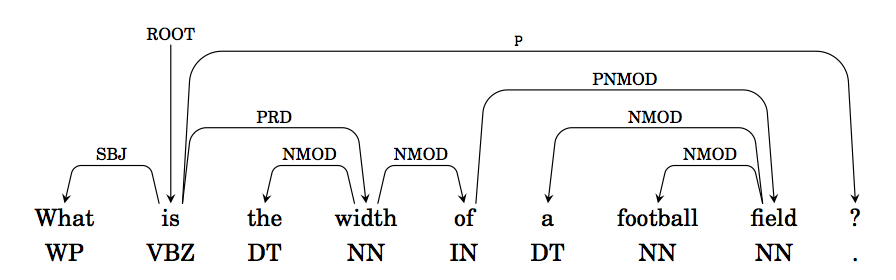
The parse automatically extract linguistic information, such as the Part-of-speech tag (e.g., field is a Noun, whosePart-of-speech tag is NN) or Dependency Relations among words (e.g., football in a Noun Modifier of field). A Dependency Parse tree can be (quite easily) manipulated and converted in tree structures that can be used by tree kernels defined in KeLP (Croce et al, 2011): a GRCT is a tree where PoS-Tags are children of grammatical function nodes and fathers of their associated lexicals.

In order to apply a tree kernel, we first need to load a dataset, where each example contains a Tree Representation. The GRCT representation of the previous parsed sentence is:

The GRCT representation is thus a representation of a tree with round brackets. Note that, the boundaries for a Tree Representation is |BT| |ET|. To automatically generate GRCT representations (or other tree representations) from text snippets please refer to this page. In this example, each question is associated to a class reflecting the aim of the question: in this case the question expects an answer with a number, i.e., NUM.
The :grct are used in KeLP to assign a label to each representation. During the kernel definition phase, these labels are used to indicate which representation must be used during the kernel computation.

The following code, reads a dataset compliant with these representations. Notice that this example is derived from the kelp-full project, from the class

and the training / test dataset are contained in the folder

So, first we load the datasets with

Then we can define a Partial Tree Kernel (PTK, [Moschitti, 2006]) with some default parameters (refers to the documentation for details).

In this example, the learning algorithm used is a SVM implementation based on the C-SVM implementation of LibSVM.

The Question Classification task addressed here is a multi-classification problem, where each question has to be associated to one class from a closed set. Here, we introduce also the concept of multi-classification. A One-vs-All classifier is instantiated. It must know what is the base algorithm to be applied, and what are the labels to be learned.
The OneVsAllLearning class will be responsible to “copy” the base algorithms, and to perform the learning according to the One-Vs-All strategy.

Then, a PredictionFunction can be obtained, in particular a OneVsAllClassifier object. This can be easily used to classify each example from the test set and evaluate a performance measure, such as the accuracy.

The tree kernels introduced in previous section perform a hard match between nodes when comparing two substructures. In NLP tasks, when nodes are words, this strict requirement reflects in a lack a lexical generalization: words are considered mere symbols and their semantics is completely neglected.

To overcome this issue, KeLP also implements more expressive tree kernel functions, such as the Smoothed Partial Tree Kernel (SPTK,[Croce et al. 2011]), that allow to to generalize the meaning of single words by replacing them with Word Embeddings that are automatically derived from the analysis of large-scale corpora. A SPTK can be implemented with the following code:

The main limitations of this approach are that (i) lexical semantic information only relies on the vector metrics applied to the leaves in a context free fashion and (ii) the semantic compositions between words is neglected in the kernel computation, that only depends on their grammatical labels.

In [Annesi et al. 2014] a solution for overcoming these issues is proposed. The pursued idea is that the semantics of a specific word depends on its context. For example, in the sentence, “What instrument does Hendrix play?”, the role of the word instrument is fully captured if its composition with the verb play is taken into account. Such reasoning can be embedded directly into the tree structures, such as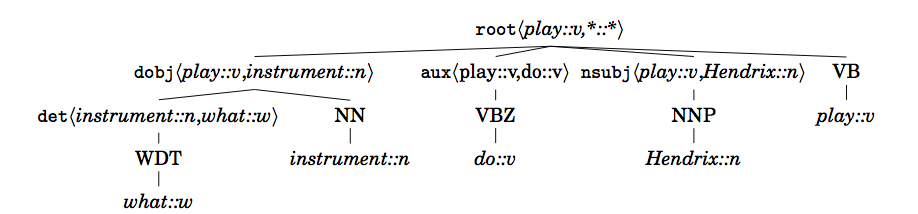 

This representation is a compositional extension of the GRCT structure (the cGRCT), where each grammatical function node n is marked adding to its original label $d_n$ (i.e., the dependency relation it represents) its underlying head/modifier pair $(h_n, m_n)$. In this case KeLP implement the Compositionally Smoothed Partial Tree Kernel (CSPTK, [Annesi et al., 2014]), that applies measure of Compositional Distributional Semantics over $(h_n, m_n)$ pairs. It can be used with the following code

The SPTK and CSPTK are very promising kernels, as they allow obtaining state-of-the-art results in the Question classification task, i.e., 95% of accuracy over well known datasets.

NOTE: even if very expressive these kernel show a computational complexity that is higher w.r.t. kernels operating over feature vectors. A caching policy is highly recommended.

Sequence Kernels

It will be available soon… stay tuned!

 

Graph Kernels

Graphs are a powerful way to represent complex entities in learning problems.
This example shows how to apply a graph kernel to a small-sized popular benchmark dataset for graphs: MUTAG (Debnath et al., 1991). The examples are chemical compounds and the task is to discriminate whether they are mutagenic/non-mutagenic.

An example in the dataset has the following form:

 
Notice that the representation delimiters are |BG|, |EG| and the representation name is inline. The task is a binary classification one.

We perform a 10-fold cross validation on MUTAG dataset using two graph kernels.
The following code is derived from the class

in the kelp-full project.

The dataset can be found in the folder

We start by loading the dataset

Two graph kernels are applied: Weisfeiler-Lehman Subtree kernel (Shervashidze et al., 2011) and the Shortest Path kernel (Borgwardt et al., 2005).

We first extract the features corresponding to the Weisfeiler-Lehman Subtree Kernel for Graphs.
The kernel counts the number of identical subtree patterns obtained by breadth-first visits where each node can appear multiple times. The depth of the visits is a parameter of the kernel, in this example it is set to 4.
The new features that are extracted will be identified by the representation name “wl”

We define next a kernel which combines the Weisfeiler-Lehman Subtree and Shortest Path kernels on the “wl” and “inline” representations. The weights of the combination are 1. We further define a cache for the kernel computations.

We define the SVM solver and an utility object for evaluating a binary SVM classifier.

The following code performs the 10-fold cross validation and reports the mean accuracy.

The mean accuracy over the ten folds is 0.8468714.

References

K. Borgwardt and H.-P. Kriegel, “Shortest-Path Kernels on Graphs,” in ICDM, Los Alamitos, CA, USA: IEEE, 2005, pp. 74–81.

Paolo Annesi, Danilo Croce, and Roberto Basili. Semantic compositionality in tree kernels. In Proceedings of the 23rd ACM International Conference on Conference on In- formation and Knowledge Management, CIKM ’14, pages 1029–1038, New York, NY, USA, 2014. ACM.

Michael Collins and Nigel Duffy. Convolution kernels for natural language. In Proceedings of the 14th Conference on Neural Information Processing Systems, 2001.

Danilo Croce, Alessandro Moschitti, and Roberto Basili. Structured lexical similarity via convolution kernels on dependency trees. In Proceedings of EMNLP, Edinburgh, Scotland, UK., 2011.

Debnath, A.K. Lopez de Compadre, R.L., Debnath, G., Shusterman, A.J., and Hansch, C. (1991). Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds. Correlation with molecular orbital energies and hydrophobicity. J. Med. Chem. 34:786-797.

Alessandro Moschitti. Efficient convolution kernels for dependency and constituent syntactic trees. In ECML, Berlin, Germany, September 2006.

Shervashidze, Nino and Schweitzer, Pascal and van Leeuwen, Erik Jan and Mehlhorn, Kurt and Borgwardt, Karsten M., “Weisfeiler-lehman graph kernels,” JMLR, vol. 12, pp. 2539–2561, 2011.